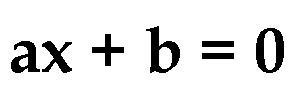Координатная прямая.
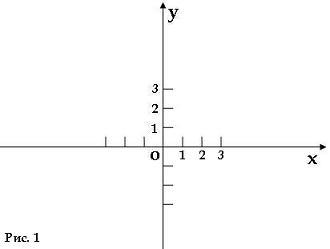
Возьмем обычную прямую. Назовем ее прямая x (рис.1). Выберем на этой прямой точку отсчета O, а также стрелкой укажем положительное направление этой прямой (рис. 2). Таким образом, справа от точки O у нас будут положительные числа, а слева – отрицательные. Выберем масштаб, то есть размер отрезка прямой, равный единице. У нас получилась координатная прямая (рис. 3). Каждому числу соответствует определенная единственная точка на этой прямой. Причем это число называют координатой этой точки. Поэтому прямая и называется координатной. А точка отсчета O называется началом координат.


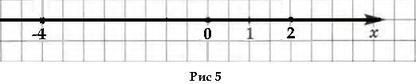
К примеру, на рис. 4 точка B находится на расстоянии 2 правее начала координат. Точка D находится на расстоянии 4 левее начала координат. Соответственно точка B имеет координату 2, а точка D координату -4. Сама точка O, будучи точкой отсчета, имеет координату 0 (нуль). Записывается это обычно так: O(0), B(2), D(-4). А чтобы постоянно не говорить «точка D с координатой такой-то», говорят проще: «точка 0, точка 2, точка -4». А саму точку при этом достаточно обозначить ее координатой (рис. 5).

Зная координаты двух точек координатной прямой, мы всегда можем вычислить расстояние между ними. Допустим, у нас две точки A и B с координатами a и b соответственно. Тогда расстояние между ними будет |a - b|. Запись |a - b| читается как «a минус b по модулю» или «модуль разности чисел a и b».
Что такое модуль?
Алгебраически модуль числа x – это неотрицательное число. Обозначается как |x|. Причем если x > 0, то |x| = x. Если x < 0, то |x| = -x. Если x = 0, то |x| = 0.
Геометрически модуль числа x – это расстояние между точкой и началом координат. А если есть две точки с координатами x1 и x2, то |x1 - x2| - это расстояние между этими точками.
Модуль также называют абсолютной величиной.
О чем еще мы можем сказать, когда речь идет о координатной прямой? Конечно о числовых промежутках.
Виды числовых промежутков.
Открытый луч.
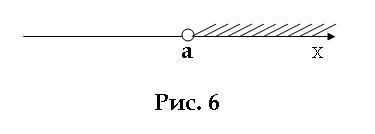
Допустим у нас два числа a и b. Причем b > a (b больше a). На координатной прямой это означает, что точка b находится правее точки a. Заменим в нашем неравенстве b на переменную x. То есть x > a. Тогда x – это все числа, которые больше числа a. На координатной прямой это соответственно все точки правее точки a. Эта часть линии заштрихована (рис. 6). Такое множество точек называют открытым лучом, а данный числовой промежуток обозначают (a; +∞), где знак +∞ читается как «плюс бесконечность». Обратите внимание, что сама точка a не входит в данный промежуток и обозначается светлым кружком.
Замкнутый луч.
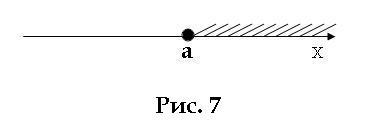
Рассмотрим также случай, когда x ≥ a. Тогда x – это все числа, которые больше или равны a. На координатной прямой это все точки правее а, а также сама точка a (на рис. 7 точка a уже обозначается темным кружком). Такое множество точек называют замкнутым лучом (или просто лучом), а данный числовой промежуток обозначают [a; +∞). Обратите внимание, что мы использовали квадратную скобку, что означает, что a принадлежит данному промежутку.
Интервал.
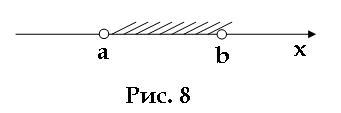
Теперь возьмем двойное строгое неравенство a < x < b. Здесь x - это все числа, которые больше a, а также меньше b. На координатной прямой это все точки между точками a и b (рис. 8). Такое множество точек называют интервалом, а данный числовой промежуток обозначают (a; b).
Полуинтервал.
Немного видоизменим наше неравенство a ≤ x < b. Здесь x - это все числа, которые больше или равны a, а также меньше b. На координатной прямой это все точки между точками a и b (рис. 9) а также еще точка a. Такое множество точек называют полуинтервалом, а данный числовой промежуток обозначают [a; b).
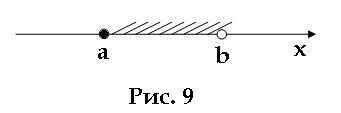
Отрезок.
Наконец возьмем двойное нестрогое неравенство a ≤ x ≤ b. Здесь x - это все числа, которые больше или равны a, а также меньше или равны b. На координатной прямой это все точки между точками a и b (рис. 10), а также сами точки a и b. Такое множество точек называют отрезком, а данный числовой промежуток обозначают [a; b].
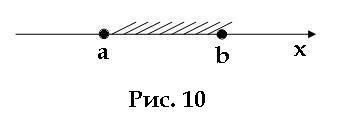
Координатную прямую также называют координатной осью. Или просто осью x.
Дата публикации:
Теги: алгебра :: геометрия :: 7 класс :: координатная прямая :: модуль числа
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
Предыдущие статьи: