Название: Методы решения уравнений высших степеней.
Возвратные уравнения нечетной степени.
Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной
степени, т.к у любого возвратного уравнения нечетной степени один из корней всегда равен -1.
уравнение
Задачи по математике, уравнения и неравенства - Вавилов В.В., Мельников И.И., Олехник С.Н.
Название: Задачи по математике - Уравнения и неравенства.
Автор: Вавилов В.В. Мельников И.И. Олехник С.Н.
1987.
Настоящая книга представляет собой справочное пособие, содержащее систематическое изложение методов решения уравнений и неравенств с одним неизвестным: иррациональных, логарифмических и показательных уравнений и неравенств, а также уравнений и неравенств, содержащих знак абсолютной величины.
Теоретическую основу составляют понятия равносильного перехода и эквивалентности двух уравнений или неравенств.
Купить бумажную или электронную книгу и скачать и читать Задачи по математике, уравнения и неравенства - Вавилов В.В., Мельников И.И., Олехник С.Н.Автор: Вавилов В.В. Мельников И.И. Олехник С.Н.
1987.
Настоящая книга представляет собой справочное пособие, содержащее систематическое изложение методов решения уравнений и неравенств с одним неизвестным: иррациональных, логарифмических и показательных уравнений и неравенств, а также уравнений и неравенств, содержащих знак абсолютной величины.
Теоретическую основу составляют понятия равносильного перехода и эквивалентности двух уравнений или неравенств.

Уравнения и неравенства - Нестандартные методы решения, справочник, Олехник С.Н., Потапов М.К., Пасиченко П.И.
Название: Уравнения и неравенства - Нестандартные методы решения - Справочник
Автор: Олехник С.Н., Потапов М.К., Пасиченко П.И.
Справочник посвящен задачам, которые для школьников считаются задачами повышенной трудности, требующим нестандартных методов решений. Приводятся методы решений уравнений и неравенств, основанные на геометрических соображениях, свойствах функций (монотонности, ограниченности, четности), применении производной. Книга ставит своей целью познакомить школьников с различными, основанными на материале программы общеобразовательной средней школы, методами решения, казалось бы трудных задач, проиллюстрировать широкие возможности использования хорошо усвоенных школьных знаний и привить читателю навыки употреблять нестандартные методы рассуждений при решении задач. Для школьников, абитуриентов, руководителей математических кружков, учителей и всех любителей решать задачи.
Скачать и читать Уравнения и неравенства - Нестандартные методы решения, справочник, Олехник С.Н., Потапов М.К., Пасиченко П.И.Автор: Олехник С.Н., Потапов М.К., Пасиченко П.И.
Справочник посвящен задачам, которые для школьников считаются задачами повышенной трудности, требующим нестандартных методов решений. Приводятся методы решений уравнений и неравенств, основанные на геометрических соображениях, свойствах функций (монотонности, ограниченности, четности), применении производной. Книга ставит своей целью познакомить школьников с различными, основанными на материале программы общеобразовательной средней школы, методами решения, казалось бы трудных задач, проиллюстрировать широкие возможности использования хорошо усвоенных школьных знаний и привить читателю навыки употреблять нестандартные методы рассуждений при решении задач. Для школьников, абитуриентов, руководителей математических кружков, учителей и всех любителей решать задачи.

Уравнения в школьном курсе математики - Бекаревич А.Н.
Название: Уравнения в школьном курсе математики. 1968.
Автор: Бекаревич А.Н.
В пособии рассмотрены наиболее важные вопросы методики преподавания уравнений в средней школе. Особое внимание автор обращает на научность их изложения, дает обоснование способов решения уравнений и их систем, начиная линейными и кончая тригонометрическими. Книга предназначена для учителей математики.
Скачать и читать Уравнения в школьном курсе математики - Бекаревич А.Н.Автор: Бекаревич А.Н.
В пособии рассмотрены наиболее важные вопросы методики преподавания уравнений в средней школе. Особое внимание автор обращает на научность их изложения, дает обоснование способов решения уравнений и их систем, начиная линейными и кончая тригонометрическими. Книга предназначена для учителей математики.

Задачи по алгебре, арифметике и анализу, Прасолов В.В.
Задачи по алгебре, арифметике и анализу - Прасолов В.В. - 2005.
Для школьников, преподавателей математики, руководителей математических кружков, студентов пединститутов.
Купить бумажную или электронную книгу и скачать и читать Задачи по алгебре, арифметике и анализу, Прасолов В.В.
Для школьников, преподавателей математики, руководителей математических кружков, студентов пединститутов.
Иррациональные уравнения, Варшавский И.К.
Иррациональные уравнения - Варшавский И.К.
Одной из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные
уравнения, так как отсутствуют общие алгоритмы их решения и приходится делать преобразования,
приводящие к уравнениям, не равносильным данному. Рассмотрим приемы решений некоторых
иррациональных уравнений.
I. Всегда ли нужно начинать решение такого уравнения
с нахождения его области опредения?
II. Случаи, когда проще свести решие уравние к решению следствия и проверке. Следствия могут быть
получены:
1. Последовательным возведением исходного уравнения в степень
2. Заменой исходного уравнения системой уравнений
3. Умножением обеих части исходного уравнения на разность радикалов
4. Использованием монотонности функций в левой части уравнения
5. Использованием подстановок, сводящих исходное уравнение к рациональному
Скачать и читать Иррациональные уравнения, Варшавский И.К.Одной из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные
уравнения, так как отсутствуют общие алгоритмы их решения и приходится делать преобразования,
приводящие к уравнениям, не равносильным данному. Рассмотрим приемы решений некоторых
иррациональных уравнений.
I. Всегда ли нужно начинать решение такого уравнения
с нахождения его области опредения?
II. Случаи, когда проще свести решие уравние к решению следствия и проверке. Следствия могут быть
получены:
1. Последовательным возведением исходного уравнения в степень
2. Заменой исходного уравнения системой уравнений
3. Умножением обеих части исходного уравнения на разность радикалов
4. Использованием монотонности функций в левой части уравнения
5. Использованием подстановок, сводящих исходное уравнение к рациональному
Обобшающий урок по геометрии - Метод координат - 9 класс
Обобшающий урок по геометрии - Метод координат - 9 класс
Цели урока:
систематизировать знания учащихся;
совершенствовать навыки решения задач методом координат;
подготовить учащихся к контрольной работе.
Оборудование:
интерактивная доска,
презентация “Метод координат на плоскости”.
Ход урока
1. Сообщение темы и цели урока.
Сообщается, что в ходе урока ученики будут набирать баллы и получат оценку в конце урока.
2. Вступительное слово учителя и сообщение учащегося из истории математики о Рене Декарте.
В это время на доске демонстрируется портрет ученого (слайд 2).
Текст сообщения (источник: Википедия):
Рене Декарт - французский математик, физик, физиолог и философ, создатель знаменитого метода координат, сторонник аналитического метода в математике, механизма в физике, предтеча рефлексологии.
Рене Декарт происходил из старинного дворянского рода. Его мать умерла от туберкулеза, когда ему исполнился 1 год. Отец Декарта был судьей и он мечтал видеть своего сына юристом. В возрасте 10 лет мальчик поступает в школу, а после ее окончания учится в Университете в Пуатье. Получив звание бакалавра и лицензию юриста , Рене выполнил желание отца, но в своей жизни он никогда не занимался юридической практикой. Он хочет видеть мир и открывать истину.
В истории математики Рене Декарт занимает видное место. Именно он сыграл решающую роль в становлении современной алгебры тем, что ввел буквенные символы, обозначил последними буквами латинского алфавита (х, у,z … ) переменные величины, а известные - первыми буквами латинского алфавит (а,b,c… ) ввел нынешнее обозначение степеней , заложил основы теории уравнений. Понятия числа и величины, ранее существовавшие раздельно, тем самым были объединены.
Историческое значение Декартовой геометрии состоит в том, что здесь была открыта связь величины и функции, что преобразовало математику. Применение алгебраических методов к геометрическим объектам, введение системы прямолинейных координат означало создание аналитической геометрии, объединяющей геометрические и арифметические величины, которые со времен древнегреческой математики существовали в раздельности.
Физические исследования относятся главным образом к механике, оптике и строению Вселенной.
Крупнейшим открытием Декарта, ставшим фундаментальным для последующей психологии, можно считать понятие о рефлексе и рефлекторной деятельности.
Интересно, что великий русский физиолог Иван Павлов поставил памятник-бюст Декарту возле своей лаборатории, потому что считал Декарта предтечей своих исследований.
Скачать и читать Обобшающий урок по геометрии - Метод координат - 9 классЦели урока:
систематизировать знания учащихся;
совершенствовать навыки решения задач методом координат;
подготовить учащихся к контрольной работе.
Оборудование:
интерактивная доска,
презентация “Метод координат на плоскости”.
Ход урока
1. Сообщение темы и цели урока.
Сообщается, что в ходе урока ученики будут набирать баллы и получат оценку в конце урока.
2. Вступительное слово учителя и сообщение учащегося из истории математики о Рене Декарте.
В это время на доске демонстрируется портрет ученого (слайд 2).
Текст сообщения (источник: Википедия):
Рене Декарт - французский математик, физик, физиолог и философ, создатель знаменитого метода координат, сторонник аналитического метода в математике, механизма в физике, предтеча рефлексологии.
Рене Декарт происходил из старинного дворянского рода. Его мать умерла от туберкулеза, когда ему исполнился 1 год. Отец Декарта был судьей и он мечтал видеть своего сына юристом. В возрасте 10 лет мальчик поступает в школу, а после ее окончания учится в Университете в Пуатье. Получив звание бакалавра и лицензию юриста , Рене выполнил желание отца, но в своей жизни он никогда не занимался юридической практикой. Он хочет видеть мир и открывать истину.
В истории математики Рене Декарт занимает видное место. Именно он сыграл решающую роль в становлении современной алгебры тем, что ввел буквенные символы, обозначил последними буквами латинского алфавита (х, у,z … ) переменные величины, а известные - первыми буквами латинского алфавит (а,b,c… ) ввел нынешнее обозначение степеней , заложил основы теории уравнений. Понятия числа и величины, ранее существовавшие раздельно, тем самым были объединены.
Историческое значение Декартовой геометрии состоит в том, что здесь была открыта связь величины и функции, что преобразовало математику. Применение алгебраических методов к геометрическим объектам, введение системы прямолинейных координат означало создание аналитической геометрии, объединяющей геометрические и арифметические величины, которые со времен древнегреческой математики существовали в раздельности.
Физические исследования относятся главным образом к механике, оптике и строению Вселенной.
Крупнейшим открытием Декарта, ставшим фундаментальным для последующей психологии, можно считать понятие о рефлексе и рефлекторной деятельности.
Интересно, что великий русский физиолог Иван Павлов поставил памятник-бюст Декарту возле своей лаборатории, потому что считал Декарта предтечей своих исследований.
Презентация по математике - Эконометрика - Уравнение множественной регрессии - Теорема Гаусса-Маркова
Презентация по математике - Эконометрика - Уравнение множественной регрессии - Теорема Гаусса-Маркова
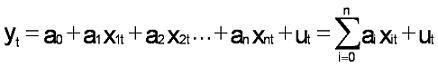
Наилучшая линейная процедура получения оценок параметров уравнения (7.1) и условия, при которых эта процедура дает несмещенные и эффективные оценки, сформулирована в теореме Гаусса-Маркова
Скачать и читать Презентация по математике - Эконометрика - Уравнение множественной регрессии - Теорема Гаусса-Маркова
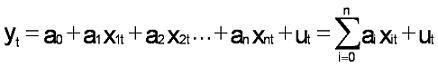
Наилучшая линейная процедура получения оценок параметров уравнения (7.1) и условия, при которых эта процедура дает несмещенные и эффективные оценки, сформулирована в теореме Гаусса-Маркова
Другие статьи...
- Презентация по математике - Алгебраические уравнения произвольных степеней
- Элементарная математика, Кеда О.А.
- Математика, Сборник тестов ЕГЭ 2009, Клово А.Г., Мальцев Д.А.
- Математика, ЕГЭ 2009, шаг за шагом Мальцев Д.А., Мальцев А.А., Клово А.Г.
- Как решать задачи по математике на вступительных экзаменах, Мельников И.И., Сергеев И.Н., 1990
- Математика в примерах и задачах, часть 1, алгебраические уравнения и неравенства, Функции, Логарифмы, Майсеня Л.И., 2006
- Алгебра и начала анализа 10-11 классы, учебник, Мордкович А.Г. - 2001
- Полный сборник решений задач для поступающих в ВУЗы, группа В, Сканави М.И., 2003
Показана страница 5 из 7
